
Como “pontapé inicial”, uma breve descrição de dicionário mostra o significado do termo “postulado” como “o que se considera como fato reconhecido e ponto de partida, implícito ou explícito, de uma argumentação; premissa”. A computação quântica toma como ponto de partida formalizações matemáticas da mecânica quântica, que vêm sendo trabalhadas pelo menos desde a década de 1930 com os axiomas Dirac-von Neumann.

Para o presente texto, me baseei fortemente nas notas do prof. Robert L. Jaffe para a disciplina 8.05 Quantum Physics II, ministrada em 1996 no MIT. As notas do Prof. Jaffe podem ser encontradas aqui. Relembrando que já fazem parte desta série, os textos “Introdução” e “Processador Eagle”. Como o assunto é um tanto complexo, não há como evitar usar notação matemática. Mas, acredite. Ela será usada na tentativa de diminuir a complexidade e não aumentá-la, uma vez que a ideia por trás da formalização matemática é clarificar o conceito abordado por meio de símbolos que representam semanticamente ideias abstratas.
É importante citar que o termo “postulados” no contexto da mecânica quântica, foi usado pela primeira vez em 1947 pelo matemático Irving Ezra Segal e mostra que, para quaisquer dois observáveis, existe um estado puro do sistema no qual eles (os observáveis) possuem valores (na realidade, expectativas de valores) diferentes [1].
Cada observável possui uma resolução espectral e um estado do sistema que induz uma distribuição de probabilidade na faixa de valores espectrais de cada um deles (novamente, dos observáveis) [2]. Os postulados de Segal são parcialmente algébricos e parcialmente métricos. A parte algébrica, define que um observável possa ser multiplicado por números reais e elevado a potências integrais, e que quaisquer dois observáveis possam ser adicionados. Já a parte métrica, define que para cada observável haja um tipo de valor numérico máximo, que desempenhe o papel de uma norma e tenha várias propriedades de acordo com seu significado físico [2].
Antes de entrar no primeiro postulado (são seis no total), vale relembrar rapidamente a notação Bra-Ket (ou notação de Dirac). A notação Ket é usada ao representarmos um estado quântico com um vetor v. É escrita como | v> (pronuncia-se “Ket v”) e denotam os vetores de coluna à direita. Por outro lado, a notação Bra é o conjugado transposto de ket, com “Bra v” escrito como <v |, denotando os vetores de linha à esquerda (Fig.1).
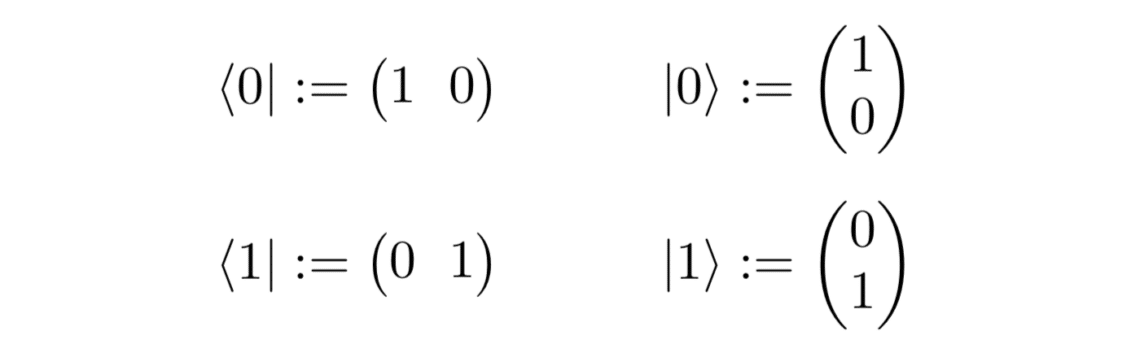
Primeiro postulado
O estado de um sistema mecânico quântico é especificado por uma função de onda, descrita por vetores unitários dentro de espaços de Hilbert, complexos e separados.
Vale comentar que um espaço de Hilbert é um espaço vetorial V (coleção de todos os vetores complexos fechados com adição vetorial e multiplicação escalar), que é dotado de um produto interno. Um estado quântico, por sua vez, é definido por uma reunião de todas as propriedades físicas de um sistema quântico, que inclui quatro propriedades principais: 1) posição, 2) momento, 3) spin (giro), e 4) polaridade.
Neste postulado, atua o princípio da incerteza de Heisenberg , o que coloca em ação o conceito de estados exclusivos. O princípio da incerteza de Heisenberg afirma que pares de valores de objetos quânticos (e.g., momento e posição) não podem ser determinados ao mesmo tempo. Isso quer dizer que, se você mede um, não pode medir o outro. Portanto, se escolhermos medir o momento de um objeto quântico, não seremos capazes de medir a posição e vice-versa.
Para clarificar, tomemos como exemplo a Fig 2. Imagine que você comprou uma pêra na feira (escrevo esse texto em uma segunda-feira, dia de feira em uma rua próxima a minha, e coincidentemente comprei algumas pêras). Resolveu jogá-la ao ar e fotografar o momento com uma câmera em que a velocidade do obturador pode ser alterada. Uma velocidade de obturação muito rápida (sem desfoque) pode dizer a localização ou posição exata em que a pêra está, mas sua aparência será fixada na foto de forma que não poderemos saber exatamente com que rapidez e nem para qual direção ela está se movendo. Se tirarmos outra foto, agora com uma velocidade de obturação lenta, o desfoque será claro e poderemos perceber a rapidez com que a pêra está se movendo, mas não a posição exata durante aquele instante.

Isso significa que a posição exata da medição da pêra e a sua velocidade exata são mutuamente exclusivas e, quanticamente, são classificadas como estados exclusivos. Com base no postulado 1, um Qbits é influenciado tanto pela base computacional, quanto pela superposição quântica. A base computacional de cálculo afirma que, como um Qbit representa dois estados exclusivos, o vetor que representa os estados quantum-0 e quantum-1 é bidimensional. Já o princípio da superposição quântica, afirma que se um sistema quântico pode estar no estado de |0>, então ele também pode estar no estado de |1>.
Em notação matemática,
|𝜓> = a|0> + b |1> = ⎡ a ⎤
⎣ b ⎦
|𝜓> (ket psi) representa um estado quântico que está na superposição de |0> ou |1> (estados 0 ou 1) e “a” e “b” representam amplitudes de probabilidade.
O estado de um sistema mecânico quântico é especificado pela função 𝜓(r, t), que depende das coordenadas da partícula “r” e do tempo “t”. Esta função é chamada de função de onda ou função de estado e tem a propriedade que 𝜓*(r, t) 𝜓(r, t) d𝞽 é a probabilidade de que a partícula se encontre no elemento de volume d𝞽 (d tau), localizado em “r” e “t”. Esta é a interpretação probabilística da função de onda, em que encontrar a partícula em algum lugar no espaço é representado por 1. Isso nos dá a condição de normalização:
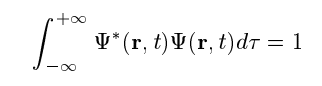
Segundo postulado
Cada atributo observável de um sistema físico é descrito por um operador que atua nos kets que descrevem o sistema.
Isso significa que, a cada partícula observável na mecânica clássica (que na computação clássica é representada por Cbit), corresponde um operador hermitiano (linear) na mecânica quântica (que na computação quântica é representada por Qbit). Este postulado vem da observação de que o valor esperado de um operador que corresponde a um observável deve ser real e, portanto, hermitiano.
Terceiro postulado
O único resultado possível da medição de um observável qualquer (e.g. A ) é um dos autovalores (eigenvalues) do operador correspondente Â.
Assim, em qualquer medição do observável associado ao operador “”, os únicos valores que sempre serão observados são os eigenvectors, “a”, que satisfazem a equação: Â𝜓 = a𝜓. Este é o postulado de que os valores das variáveis dinâmicas são “quantizados” na mecânica quântica, embora seja possível ter um continuum de eigenvalues no caso de estados não ligados. Se o sistema estiver em um eigenstate de “” com eigenvalue “a”, qualquer medição da quantidade “A” sempre produzirá o valor “a”.
Quarto postulado
Quando uma medição de um observável A é feita em um estado genérico | 𝜓>, a probabilidade de obter um eigenvalue an é dada pelo quadrado do produto interno de | 𝜓> com o eigenstate | an>, | <an | 𝜓> |².
Assim, a probabilidade de encontrar uma partícula em um determinado ponto é diretamente proporcional à magnitude da função de onda de uma partícula (localizada naquele ponto) ao quadrado. A função de onda entra em colapso em um estado imediatamente após a medição. A probabilidade de observar o eigenvalue “ai” é dada pelo valor absoluto do quadrado do coeficiente “ci” (ou seja, |ci|²). Assim, se quisermos descobrir o estado do sistema quântico, encontramos a sua probabilidade com: P(𝜑) = |<𝜑i | 𝜓i>|². A probabilidade (P phi) de medir o estado é dada pelo produto escalar da amplitude e do estado ao quadrado.
Para entender melhor, vamos aplicar esta equação a um exemplo comum, o famoso gato de Schrödinger. Assim, dentro de uma caixa lacrada está um gato, um frasco de veneno e uma fonte radioativa (vê-se logo que Schrödinger não era lá um fã de gatos). Um monitor interno também é usado para detectar radioatividade. Quando a radioatividade é detectada, o frasco libera o veneno, fato que pode matar (ou não) o gato. Nessa situação, temos a probabilidade de o gato estar vivo (1/√2) e a probabilidade de o gato estar morto (1/√2), como na Fig 3.
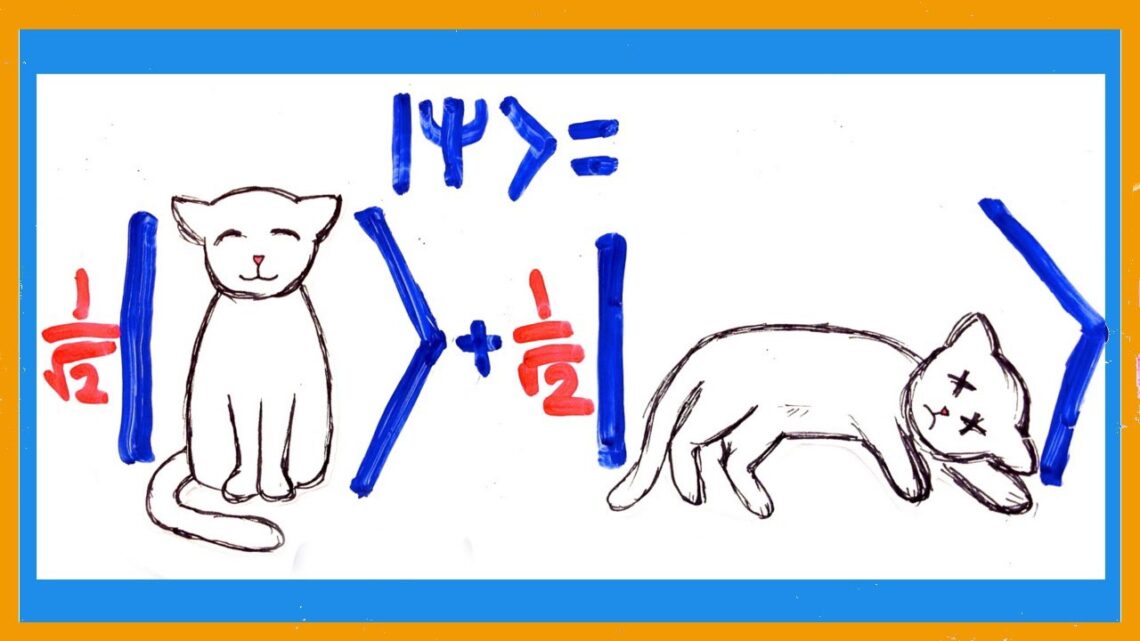
Pelo conceito de superposição, o gato pode estar morto e vivo ao mesmo tempo. Mas, se você abrir a caixa e olhar lá dentro, o estado quântico do gato colapsa em um único estado, em que o bichano está morto ou vivo (mas não ambos). Como resultado, a medição quântica é classificada a partir da regra de Born, tendo o colapso da onda como resultado. Isso pressupõe que os coeficientes usados são números reais. No entanto, também podemos usar números complexos. Os números reais em uma reta numérica só podem apontar para a esquerda ou para a direita, enquanto os números complexos podem apontar em qualquer direção, mesmo na diagonal. Assim, em uma versão muito simplificada, a probabilidade desse estado particular seria o comprimento da reta ao quadrado. O comprimento da reta pode ser escrito como d + ei. Imagine então, um plano de coordenadas onde o eixo x representa números reais (d) e o eixo y representa os números imaginários (ei), só que elevado ao quadrado. Com isso temos, P(𝜑) = |<𝜑i | 𝜓i>|² .
Quinto postulado
Imediatamente após a medição de um observável A produzir um valor an, o estado do sistema é o eigenstate normalizado |an>.
Este postulado é conhecido como o “colapso do pacote de ondas (wavepacket)”. Wavepacket é um caso particular de função de onda. Ela ocupa uma região restrita no espaço e geralmente se move em velocidade. A função de onda, neste caso, é decomposta em duas partes: um pacote refletido e em um pacote transmitido. Dessa forma, existe a probabilidade de se encontrar um fóton (ou qualquer outra partícula) em uma ou na outra parte do pacote de ondas dividido, cada vez que ele for medido. Assim, sistemas preparados de forma idêntica podem produzir resultados experimentais diferentes. É o que torna esse postulado um tanto quanto controverso, embora esse tipo de resultado seja abrangido pelo quarto postulado.
Imagine que o observável “A” foi medido com o resultado “an” em um determinado sistema e, imediatamente em seguida, novamente medido. Embora os resultados da segunda medição não sejam estatisticamente distribuídos, serão sempre “an”. Isto acontece porque o colapso do pacote de ondas (wavepacket) preserva a normalização do estado. Daí o postulado.
Sexto postulado
A evolução do tempo de um sistema quântico preserva a normalização do ket associado. A evolução temporal do estado de um sistema quântico é descrita por |𝜓(t)> = Û(t, t0) |𝜓(t0)>, para um operador unitário Û.
Basicamente, o sexto postulado diz que, sob uma evolução temporal, o estado |𝜓> move-se em um espaço de estados (i.e., espaço da função de onda) em uma trajetória definida |𝜓(t)>. A preservação da norma do estado está associada à conservação da probabilidade. Assim, para que possamos conservar amplitudes de probabilidade na computação quântica, usamos matrizes unitárias para constituir os quantum gates básicos e as operações dentro da multiplicação de matrizes. As matrizes unitárias são centrais no processo computacional quântico porque são capazes de preservar normas (e.g., funções para atribuir comprimento e tamanho estritamente positivo para cada vetor dentro do espaço vetorial). É esta preservação de normas que garante a preservação de amplitudes de probabilidade.
Com base nestes seis postulados, os Qbits podem ser manipulados pelos quantum gates. Por exemplo, o sexto postulado permite aplicar o princípio de exclusão de Pauli nos quantum gates (os chamados Pauli gates) para mudar a direção do spin de um elétron. Peguemos o gate Pauli-X, se inserirmos |0> em um Pauli-X, obteremos |1> e vice-versa. Vejamos o processo pela multiplicação de matrizes. O Pauli-X gate é representado pela seguinte matriz (𝛔x):
𝛔x = ⎡0 1 ⎤
⎣1 0 ⎦
A matriz que representa |0> é:
|0> = ⎡ 1 ⎤
⎣ 0 ⎦
Ao multiplicarmos a matriz (𝛔x) por |0>, temos:
𝛔x |0> = ⎡0 1 ⎤ ⎡ 1 ⎤ = ⎡(0) (1) + (1) (0) ⎤ = ⎡0⎤ = |1>
⎣1 0 ⎦ ⎣ 0 ⎦ ⎣(1) (1) (0) (0)⎦ ⎣1⎦
Ao aplicarmos um Pauli-X a um Qbit que está em um estado de superposição de |0> e |1>, temos o mesmo efeito:
𝛔x ⎡a⎤ = ⎡0 1 ⎤ ⎡ a ⎤ = ⎡(0) (a) + (1) (b) ⎤ = ⎡b⎤ ⎣b⎦ ⎣1 0 ⎦ ⎣ b ⎦ ⎣(1) (a) (0) (b)⎦ ⎣a⎦
Visualizando o ocorrido em uma esfera de Bloch, podemos perceber a mudança de direção do spin de | 𝜓1> para | 𝜓2> (Fig.4).
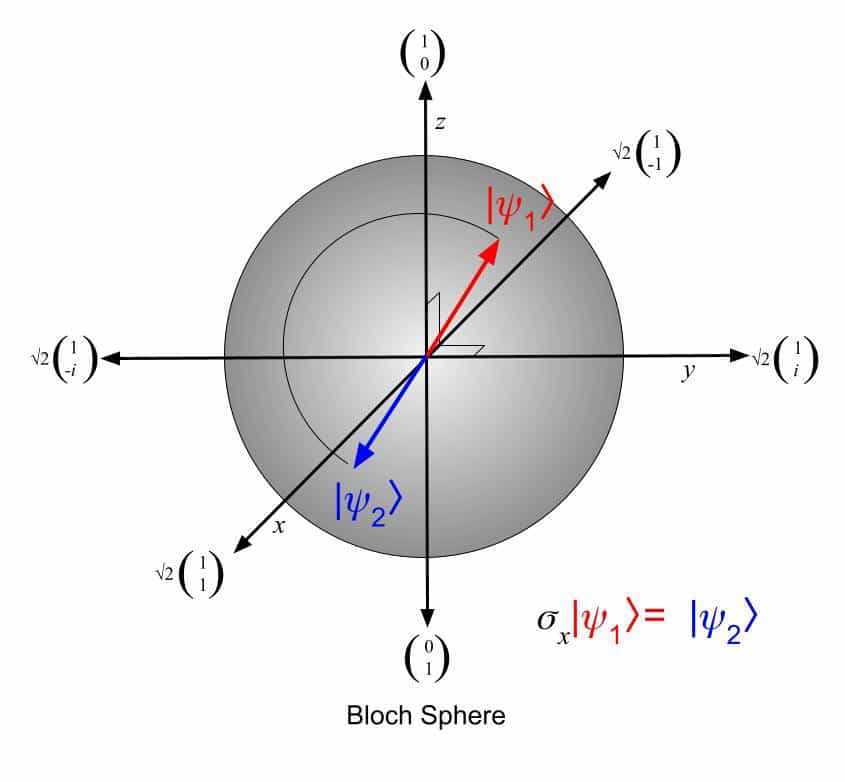
Reparem que o vetor fez uma rotação de 180º sobre o eixo x. É importante reforçar que os Qbits, por si só, não fazem muita coisa. A manipulação deles por intermédio dos quantum gates é que permite que criemos circuitos e algoritmos específicos para serem usados em computação quântica. E essa manipulação só é possível por causa dos postulados.
P.S.: Por conta de compromissos profissionais que assumi para 2022, muito possivelmente não conseguirei manter uma rotina de escrita de textos para este espaço, como fiz em 2021. No entanto, me comprometo a produzir pelo menos 2 textos específicos no primeiro semestre do próximo ano: um sobre quantum gates, para complementar este texto sobre os postulados e outro, sobre o segundo relatório do estudo de cem anos sobre inteligência artificial (AI100), publicado em 2021.
Referências
[1] Strocchi, Franco (2012) Spontaneous symmetry breaking in quantum systems. Scholarpedia, 7(1):11196.
[2] Segal, I.E. (1947). Postulates for General Quantum Mechanics. Annals of Mathematics, 48, 930.