
Resolver problemas de matemática é uma das formas mais garantidas de se desenvolver o conhecimento na matéria. Sua importância vem da crença de que a matemática se constrói a partir do raciocínio e não da memorização. Desta forma, a resolução de problemas permite que a pessoa compreenda e consiga explicar os processos usados para chegar às soluções, ao invés de se lembrar de como aplicar um conjunto de procedimentos. “É por meio da resolução de problemas que [as pessoas] desenvolvem uma compreensão mais profunda dos conceitos matemáticos, tornam-se mais engajadas e apreciam a relevância e a utilidade da matemática” [1].
Comentei em um texto anterior, a respeito do termo “heurística” e expliquei basicamente que se referia a qualquer abordagem de resolução de problemas que usa um “método prático (ou vários atalhos) para produzir soluções que podem não ser ótimas, mas são suficientes para resolver o problema”. A heurística mais usada para a resolução de problemas matemáticos foi desenvolvida pelo matemático autríaco George Pólya, que em seu livro “How to solve it, a New Aspect of Mathematical Method” [2] sugeriu quatro princípios: (1) entender e explorar o problema; (2) encontrar uma estratégia; (3) usar a estratégia para resolver o problema; e (4) revisar e refletir sobre a solução (Fig.1).
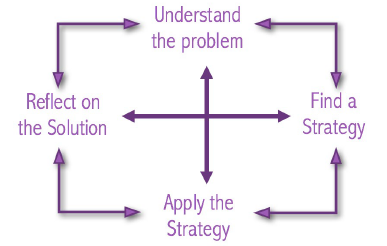
Note pela Fig. 1 que os princípios de Pólya não fazem parte de um processo linear, são etapas que podem se sobrepor ou ocorrer em paralelo. Se aproxima mais a um método. Os princípios de Pólya podem parecer simples à primeira vista, mas sua implementação requer esforço concentrado. Podemos reconhecer alguns desses esforços ao observar o trabalho das chamadas “sociedades de matemática”, como a Sociedade Brasileira de Matemática (SBM), que organiza a Olimpíada Brasileira de Matemática das Escolas Públicas (OBMEP). Além das Olimpíadas, há também as chamadas “sessões de resolução de problemas” (problem sessions), como as organizadas pela London Mathematical Society. Nessas sessões são apresentados problemas matemáticos como desafios e dado um tempo para sua resolução. Em seguida, há um debate entre os participantes a respeito de como os problemas foram solucionados. Tive a oportunidade de participar de uma dessas sessões, que trouxe um problema bem interessante, proposto na Olimpíada Britânica de Matemática de 2009. Trata-se da primeira questão da segunda rodada (quem se interessar, pode achá-la aqui), que transcrevo abaixo:
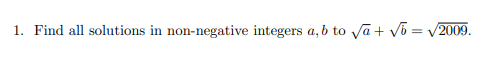
“Encontre todas as soluções de números inteiros não negativos a, b para √a + √b = √2009”.
O interessante deste problema é que ele permite que se veja a aplicação dos princípios de Pólya como um quebra-cabeça, onde tenta-se encontrar os princípios que melhor se encaixem à imagem. Vejamos, o primeiro passo que a maioria das pessoas tentaria é ajustar os dois lados da equação, elevando-a ao quadrado. Essa é a primeira dica que sempre ouvimos quando lidamos com raízes quadradas. Não tenha dúvidas de que foi o que eu tentei inicialmente. Mas, se fizermos isto com a equação do modo como ela foi apresentada, temos:
(√a + √b)² = (√2009)²
a + 2√ab + b = 2009 (1)
Bom, conseguimos reduzir o número de raízes quadradas, embora tenhamos criado um problema adicional, que foi incluir a variável √ab. Meu erro aqui foi ignorar os dois primeiros princípios de Pólya. Ao invés de correr para aplicar a primeira solução que vem a mente, é preferível se perguntar:
(i) Este é realmente o melhor método que você conhece para lidar com esse problema?
(ii) Se este é o melhor método que você conhece, o problema está definido da melhor maneira para você aplicá-lo?
Apesar de não haver nada de errado com o que tentei fazer inicialmente, a adição da variável √ab tornou as coisas mais difíceis porque, sem querer, misturei as informações fornecidas pelas variáveis a e b. Explico, inclui uma função de medida aditiva (e.g. f (x) + f (y) = f (xy)) em um problema onde isto não existia inicialmente. Este foi o primeiro ponto levantado na discussão da sessão. Ao invés de logo elevar ao quadrado os dois lados da equação, eu poderia ter a reorganizado como:
√a = √2009 – √b (2)
E aí sim, elevar ao quadrado os lados. Dessa forma, teríamos:
(√a)² = (√2009 – √b)²
a = 2009 – 2 √2009 + b (3)
Note que em (3) conseguimos reduzir o número de raízes quadradas que tínhamos sem a função de medida aditiva (as variáveis “a” e “b” continuam separadas). Isso simplifica o modo como avançaremos, porque claramente todos os termos da nossa equação são números inteiros (com a possível exceção de 2√2009b). Aqui entra o quarto princípio de Pólya (revisar e refletir sobre a solução). Neste caso, podemos aplicar o raciocínio dedutivo. Sabemos que somar ou subtrair dois inteiros sempre resulta em um outro inteiro. Com isto, podemos deduzir que √2009b é um número inteiro. Como se pode deduzir isto? Pelo próprio enunciado da questão (“Encontre todas as soluções de números inteiros não negativo…”). Assim, podemos reescrever nossa equação (3) como:
2√2009b = 2009 – a + b (4)
Existem poucos números para os quais tirar a raiz quadrada resulta em um inteiro, já que só os números quadrados perfeitos possuem raiz quadrada exata. Então, como podemos usar essa informação? Em primeiro lugar, podemos decompor o número um pouco mais e tirar o “excesso de ruído” do material. É possível notar que:
2009 = 49 X 41 = 7² X 41 (5)
Podemos então reescrever √2009b como:
√2009b = √(7²)(41b) = 7√41b (6)
Sabendo que √2009b é um número inteiro (pelo enunciado da questão), podemos inferir que √41b também o é (porque provavelmente é um número quadrado perfeito, já que a sua raiz quadrada é um número inteiro). Mas, o que significa dizer que √41b é um número inteiro? Quer dizer que devemos ter a relação 41b=c², para um número inteiro “c”. Sabemos também que √41 não é um número inteiro (a resposta é aproximadamente 6,403). Desta forma, a única maneira de √41b ser um número inteiro, é b=41d², para um número inteiro “d”. Isto nos permitiria escrever c²=41b= 41(41d²). A lógica é mantida se tivéssemos reorganizado a equação (2) com √b = √2009 – √a. Neste caso, chegaríamos a uma conclusão similar com a=41e² para um número inteiro “e”, porque estamos lidando com uma função simétrica.
Temos agora duas informações importantes: a=41e²; b=41d²; em que tanto “d” quanto “e” são números inteiros. Novamente utilizando o raciocínio dedutivo, se “a” e “b” são números inteiros não negativos (dito no enunciado da questão), “d” e “e” também o são. Voltando à equação original, temos:
√a + √b = √2009
√41e² + √41d² = √49 x 41
√41e² + √41d² = 7√41
e√41 + d√41 = 7√41
e + d = 7
Bem mais fácil para se lidar, não? Existe um número muito pequeno de possíveis soluções para essa equação de “d” e “e”. Vamos a elas (leiam como se fossem colunas):
d e
0 7
1 6
2 5
3 4
4 3
5 2
6 1
7 0
Relembrando que a=41e² e b=41d², temos:
a b
2009 0
1476 41
1025 164
656 369
369 656
164 1025
41 1476
0 2009
De acordo com Anthony e Walshaw (2007), para se estimular o raciocínio matemático e construir um conhecimento matemático durável, as pessoas “precisam ter oportunidades de trabalhar em tarefas complexas, em vez de uma série de tarefas simples derivadas de uma tarefa complexa” [3]. O foco dos princípios de Pólya é lidar com a resolução de problemas complexos pela exposição a eles. Com isso, processos de aprendizagem “onde a orientação define consistentemente os resultados da tarefa em termos de respostas, em vez dos processos de pensamento implicados em alcançar as respostas, afetam negativamente os processos de pensamento e identidades matemáticas” [3]. Lembrar dos quatro princípios antes que “cair dentro” de um problema (não necessariamente matemático), pode ajudar uma pessoa a ativamente construir suas ideias para encontrar a solução mais apropriada.
[1] Wu, M., & Zhang, D. (2006). 'An overview of the mathematics curricula in the West and the East'. In F. K. S. Leung, K, Graf & F. J. Lopez-Real (Eds.), Mathematics Education in Different Cultural Traditions – A Comparative Study of East Asia and the West (pp. 181–194). [2] Pólya, G. (1945). How to solve it. A New Aspect of Mathematical Method. Princeton University Press. [3] Anthony, G.; Walshaw, M. (2007). Effective pedagogy in mathematics: Best evidence synthesis iteration [BES]. Wellington: Ministry of Education.