
Em meu texto anterior, compartilhei uma equação que causou um certo debate entre um grupo de amigos meus. A equação em questão era a seguinte: -1 = i * i. Como foi durante o final de semana em que se comemorava o Halloween, apelidei-a com o seu nome. Como recebi diversas mensagens comentando o texto e pedindo explicações adicionais, resolvi escrever mais algumas linhas sobre o assunto.
Números Complexos
O primeiro ponto de esclarecimento se refere ao envolvimento de números complexos. Por que considerá-los parte da equação? Aqui vale uma rápida descrição. O conjunto dos números complexos é formado por números que compõem o conjunto dos números reais e uma unidade imaginária. Essa unidade foi chamada de imaginária porque quando foi descoberta por René Descartes no século XVII, muitos consideraram que se tratava de uma invenção dele. Este, aliás, é um grande debate matemático-filosófico: se a matemática foi descoberta ou inventada por nós, seres-humanos. Sou daqueles que consideram que ela foi descoberta (é a “língua” do universo, na minha opinião). Bom, o que importa para nós, nesse momento, é que a unidade imaginária dos números complexos é representada pela letra “i”.
Esta é a primeira grande dica da pequena equação de Halloween, ela é composta pela unidade imaginária. A segunda grande dica é que, ao se conhecer os números complexos e considerar que ela se encontra nesse plano, a sua resposta fica evidente pelas potências de “i”. i * i, significa que a tal unidade imaginária foi multiplicada por ela mesma, o que dá no mesmo de dizer que é um número elevado ao quadrado (i^2).
O que disse no parágrafo acima, é a minha interpretação da de Halloween. Que ela representa i^2. Mas, não quero impor a minha visão. Abaixo (Fig.1), reproduzo as quatro primeiras potências de i:
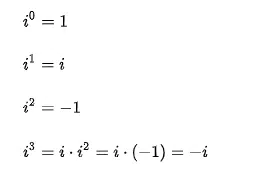
Note que i^2 é exatamente -1 e que a nossa pequena equação de halloween é apenas uma outra forma de escrevê-la. Só que é exatamente aqui que está o debate. Outros partem do princípio de que se esta unidade é imaginária, você pode imaginá-la da maneira que quiser dentro do plano cartesiano (x,y), como se o “y” fosse, de fato, um número real (o que não é verdade, se estivermos no plano de Argand). No plano de Argand, a abscissa y representa a “parte imaginária” do número complexo.
A primeira “provocação” da √-1 está dentro do pressuposto de que se a unidade é imaginária, qualquer coisa basta. Ao se estudar raiz quadrada, é comum ouvir a afirmação “não existe raiz quadrada de número negativo dentro do conjunto dos números reais”. A pegadinha aqui é que se “i” é um número imaginário, não está dentro do conjunto dos números reais. Neste caso, “i” efetivamente é √-1. Vejamos a Figura 2:
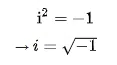
A segunda “provocação” da √-1 é considerar a sua multiplicação por si mesma como sendo √1. Isto é verdade para números reais negativos porque a negação do negativo (e.g., -1*-1) é o positivo (e.g., 1). Mas, √-1 não é um número real, é imaginário. Daí, nossa Figura 3:
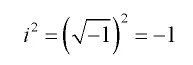
Por isso, na minha resposta preferi considerar a unidade imaginária i = √1 e incluir o sinal negativo fora da raiz quadrada. Fato que, olhando em retrospecto, também era desnecessário, já que (√-1)^2 já é -1. O interessante deste tipo de coisa é brincar com a matemática. A verdade é que não importa se ela é descoberta ou inventada, ela existe como uma das maiores ferramentas que temos para entender e explicar o que está à nossa volta (estou sendo metafísico de propósito). Minha dica é usá-la do jeito que você achar melhor, para melhor se familiarizar com ela.